This is the continuation of Spartan - Part 1. In Part-1, I have talked about the basic features that Spartan provides us. Also, I have discussed how to build molecules in Spartan (both in 2D and 3D formats), all types of models and output files available in Spartan. Furthermore, I have discussed bond breaking-bond making and energy optimization. For those, who didn’t check the Part-1 yet, please read it before going further —
In Part-2, I’ll discuss different types of parameters measuring available in Spartan. Also, I’ll discuss different types of constraining methods available in Spartan. These constraining methods are very much useful for restraining a molecule in a particular geometry and understanding its properties in that specific geometry.
⁕ ⁕ ⁕
Measuring Parameters:
We can easily measure different types of parameters like bond distance, bond angle and dihedral angle using Spartan. I’m giving a short description of how one can measure these things —
Measuring Distance:
One can measure an equilibrium bond length between 2 bonded atoms using this option. That doesn’t mean that one can not measure unoptimized bond distances using this option. But for chemistry aspects of view, one is more interested in the optimized structures’ properties. One can find this option under the Geometry option in the header section. Now after selecting the Measure Distance option one has to select 2 atoms one by one (those bonded atoms of which bond length has to be measured). Then one can see the optimized bond length between those specific atoms at the bottom-right corner of the window. Also, he’ll be able to see the labelling on the selected bonded atoms (Figure 2.1). Furthermore, one can measure between 2 non-bonded atoms also by following the same procedure.
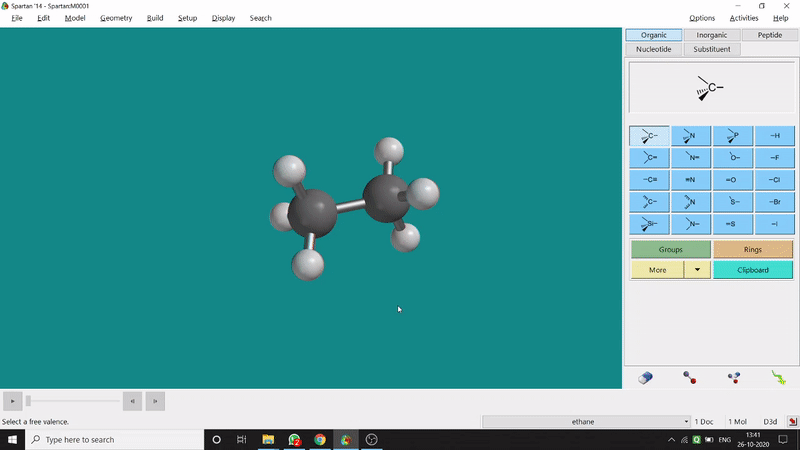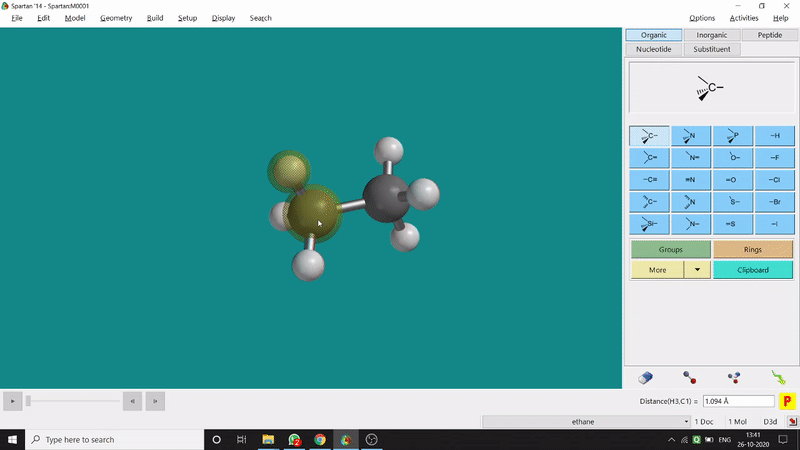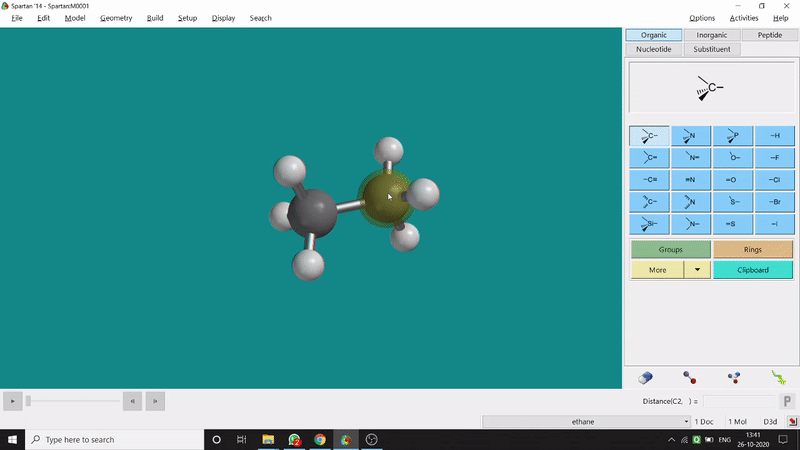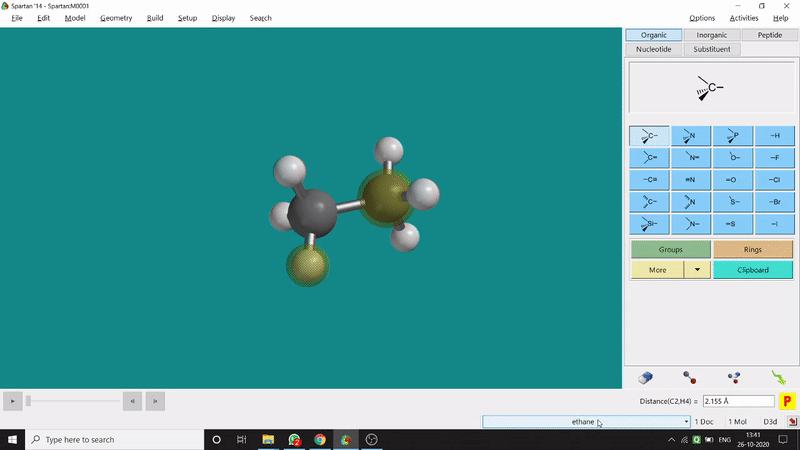
Figure 2.1: Bond distance measurement procedure
Measuring Angle:
One can measure the angle created by 3 atoms in a molecule by the Bond Angle option under the Geometry option. The 3 atoms can be bonded or non-bonded. The bond angle can be measured in the optimized state or the unoptimized state. Here also, the bond angle between those specific atoms can be seen at the bottom-right corner (Figure 2.2) of the window and labelling on the atoms can also be seen.
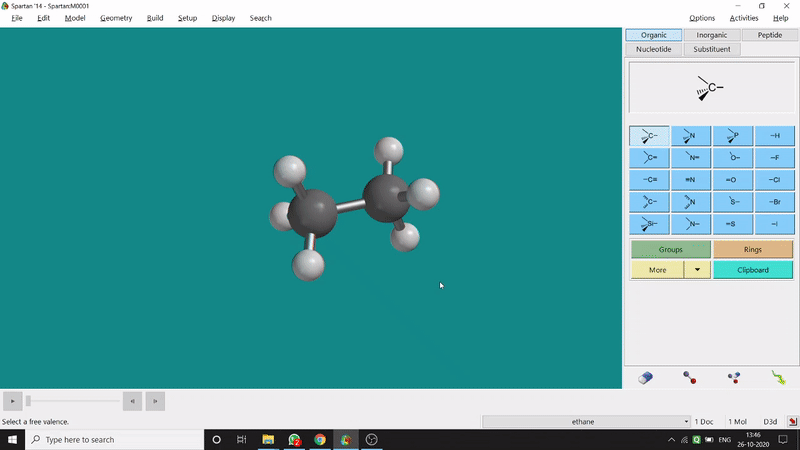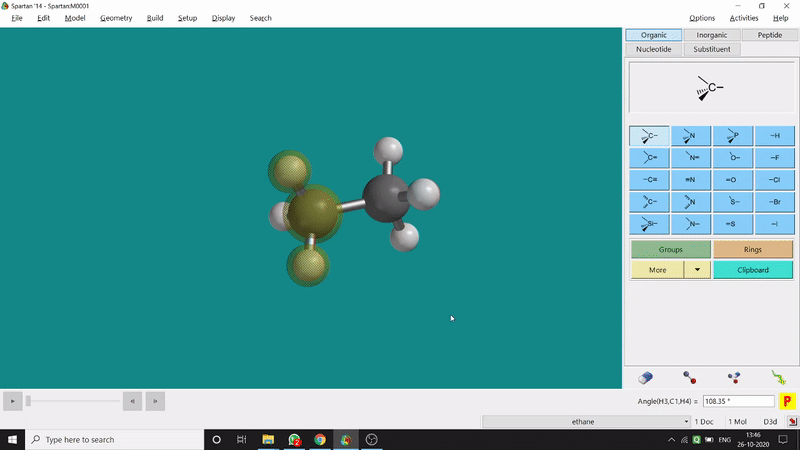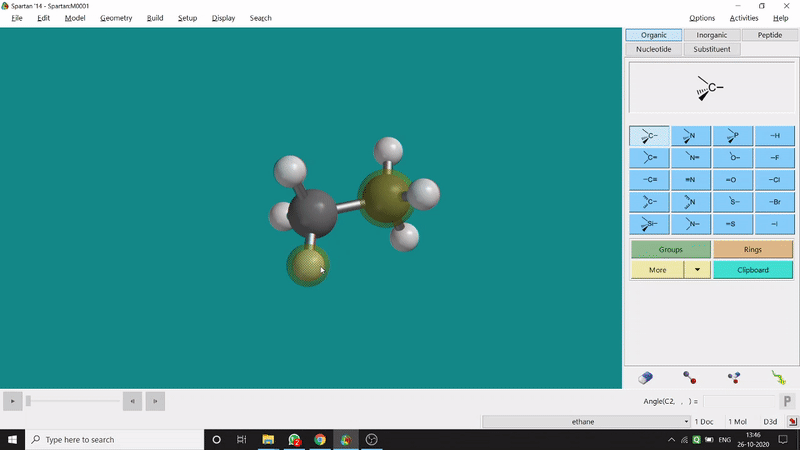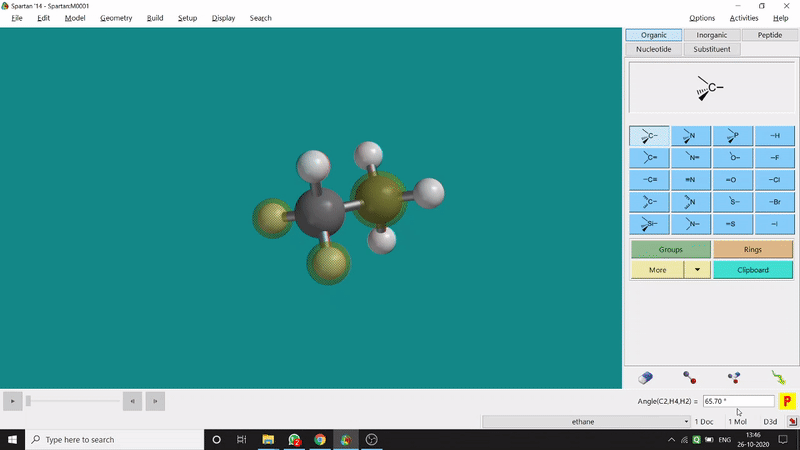
Figure 2.2: Bond angle measurement procedure
Measuring Dihedral:
The angle between two planes created by any 4 atoms in a molecule is called a dihedral angle. In Spartan, one can easily measure a dihedral angle between any two planes created by any 4 atoms (bonded or non-bonded) in a molecule. This Measure Dihedral option can also be found under the Geometry option. The calculated dihedral angle can be seen at the bottom-right corner (Figure 2.3) of the window and labelling on the atoms can also be seen.
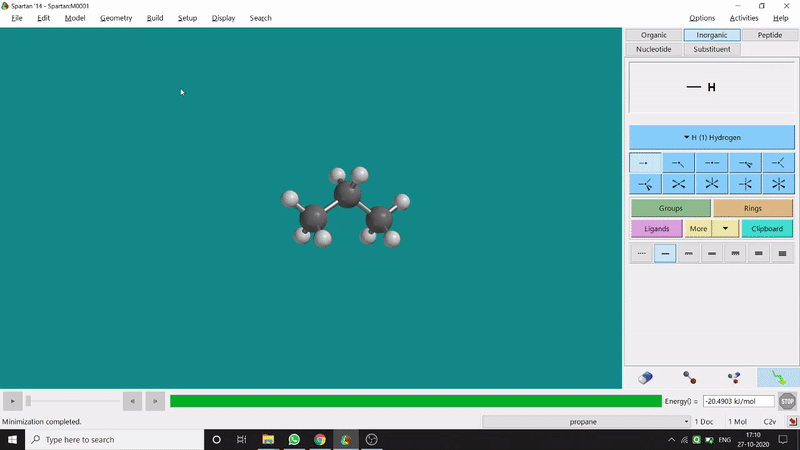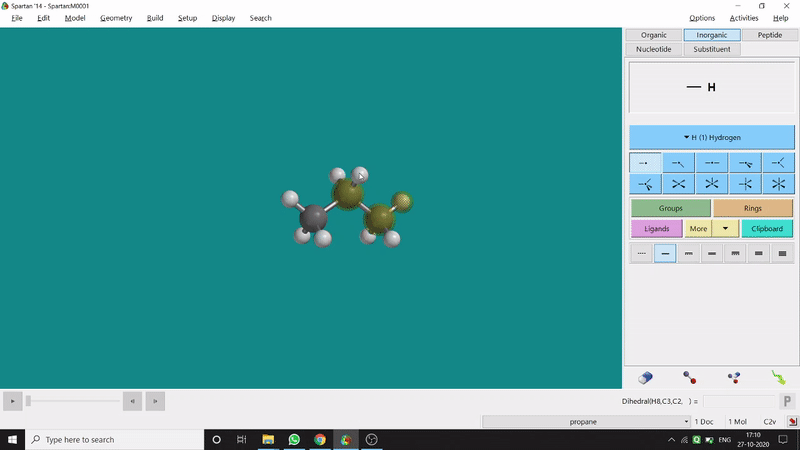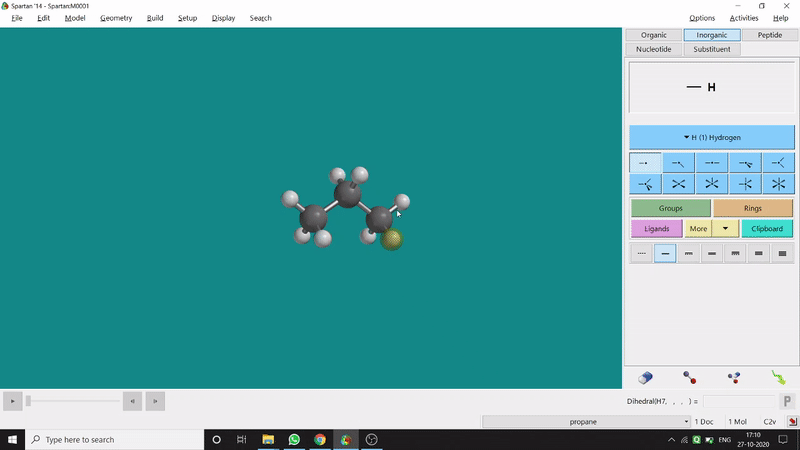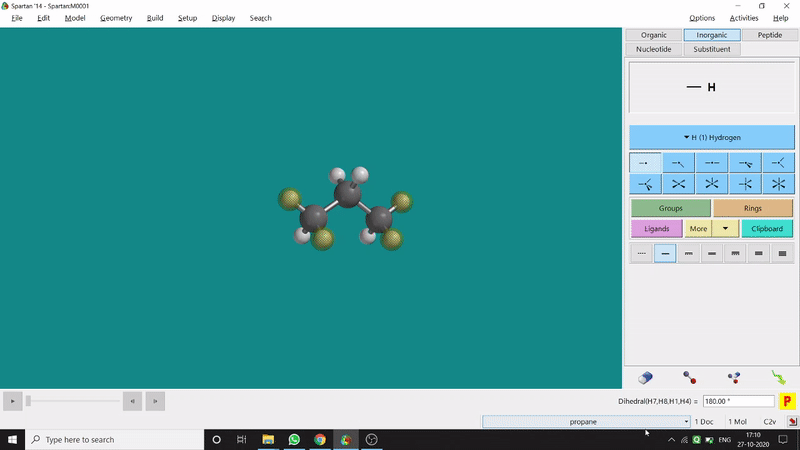
Figure 2.3: Dihedral angle measurement procedure
Constraining Parameters:
While calculating different type of data for a molecule or to gain a certain point group we have to constrain measuring parameters. It is a very very useful feature provided by Spartan for many theoretical calculations. I have described all 3 types of constraints below —
Constraining Distance:
We can constrain a bond distance to fix that as per our need. We can find this option under the Geometry option. But for constraining a bond we have to select the Measure Distance option (for those two atoms) and have to change the bond length manually. After that, we have to select the Constrain Distance option. Again we have to select those two atoms one by one. Thereafter, an open lock symbolled option can be seen at the bottom-right corner of the window. We have to click that option to restrain the bond distance. In Ethane (C2H6), the normal C — C bond distance is 1.512 Å. But I restrained it to 5 Å and for the rest of the calculation, it’ll be the same (Figure 2.4).
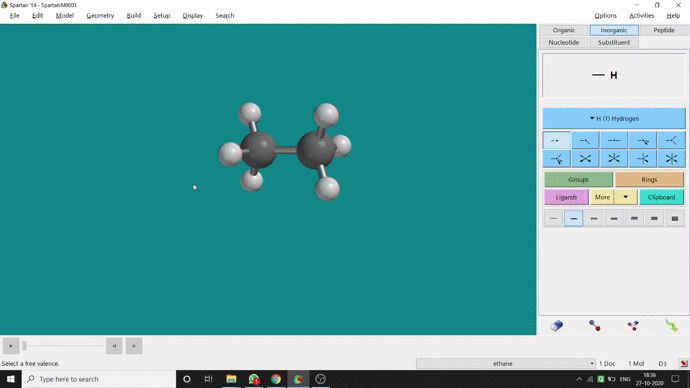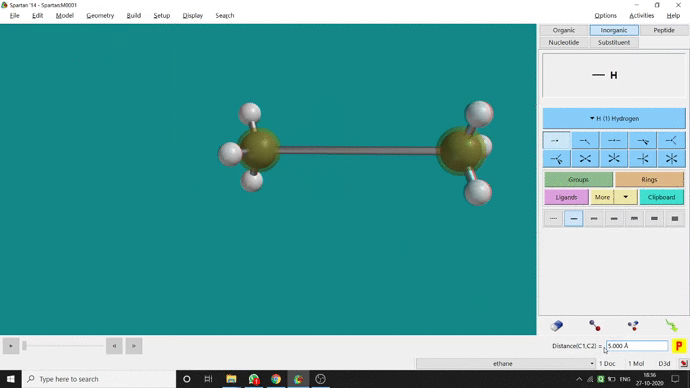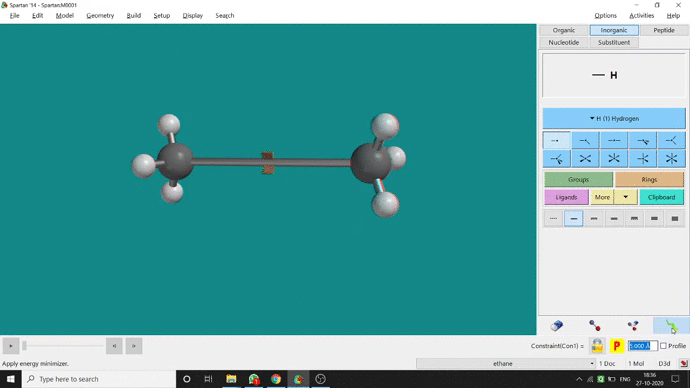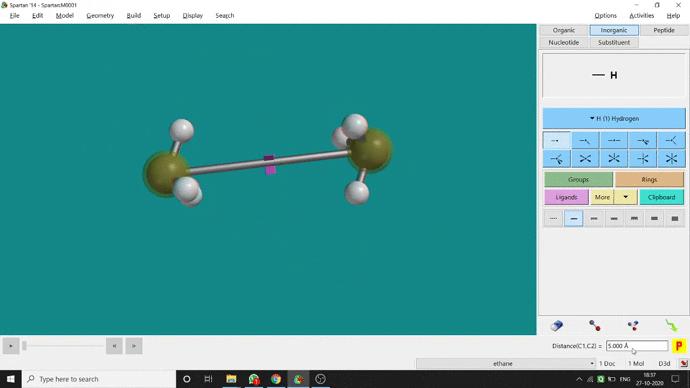
Figure 2.4: Bond distance constraining procedure
Constraining Angle:
Like constraining distance, we can also constrain angle for three atoms. The procedure is almost the same. One has to measure the bond angle using the Measure Angle option and manually change the angle. The next step is to constrain the angle using the Constrain Angle option under the Geometry option. The next step is locking the angle by clicking the open-lock symbolled option at the bottom-right corner of the window. In water (H₂O) the normal H — O — H bond angle is 103.98°. But I limited it to 180° and for the rest of the calculation, it’ll be the same (Figure 2.5).
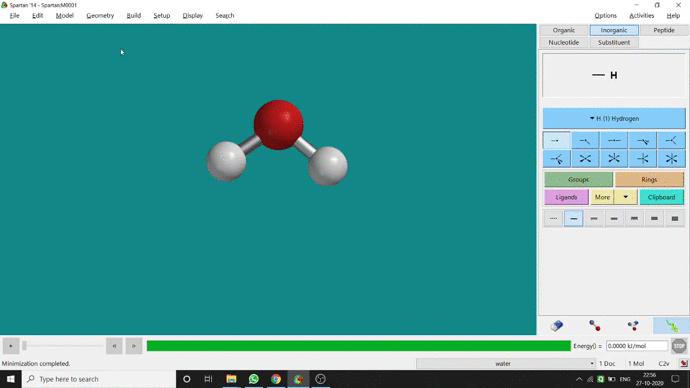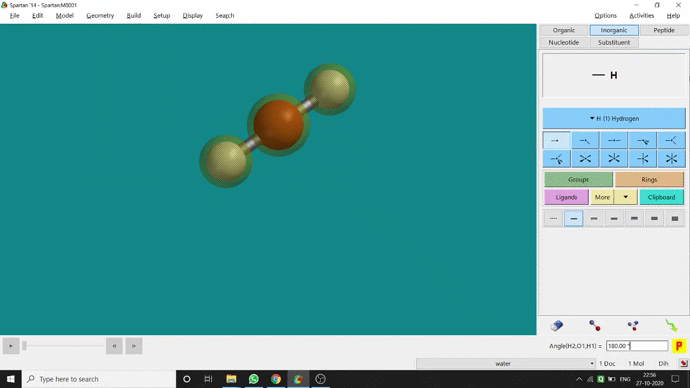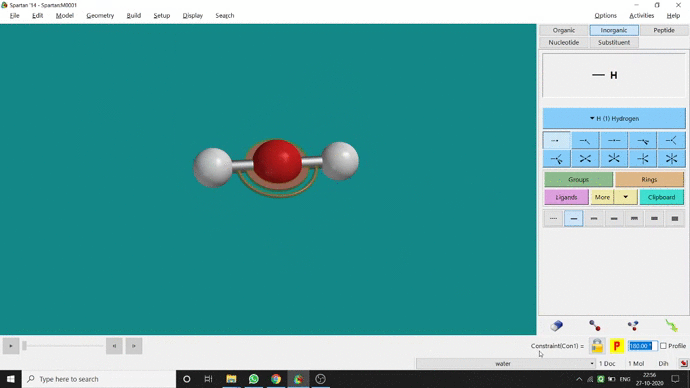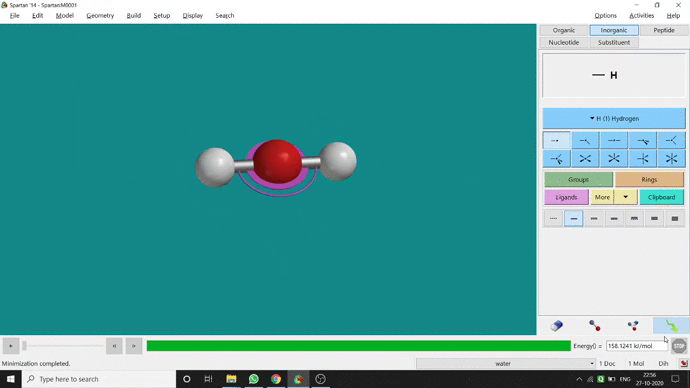
Figure 2.5: Bond angle constraining procedure
Constraining Dihedral:
In my opinion, constraining dihedral angle is the most used tool for restraining a molecule into a specific point group. Like other constraining options, the Constrain Dihedral option can be found under the Geometry option. One has to select the Measure Dihedral option followed by selecting the 4 atoms associated with the dihedral angle. The next step is giving the dihedral angle manually and constraining it by selecting the Constrain dihedral option and clicking the open-lock symbolled option at the bottom-right corner of the window. For Hydrogen Peroxide (H₂O₂), if one uses Spartan optimization, the dihedral angle will be ~129.36° (but actually it is ~111.5° in the gas phase). This difference will not come if we use good quantum methods like MP2 or B3LYP like DFT methods and we get ~111.5° dihedral angle. Whatever, if we want to restrict the dihedral angle manually (Figure 2.6) to 100° (or whatever is needed for the calculation) that will be the same for the rest of the calculations.
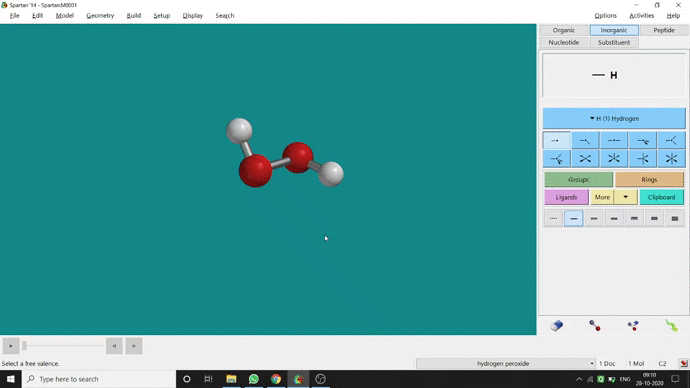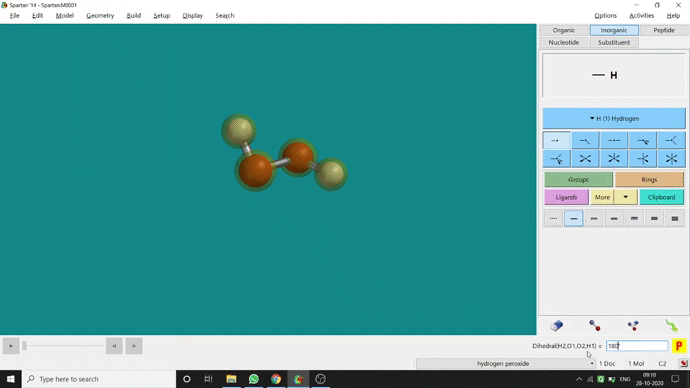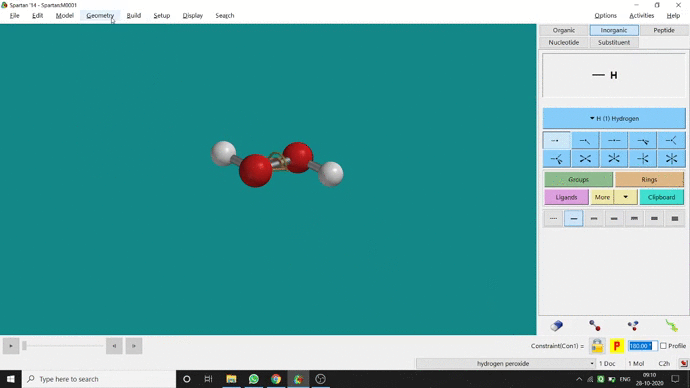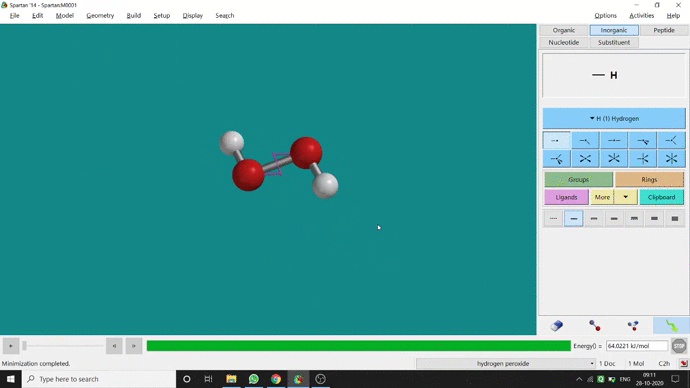
Figure 2.6: Bond dihedral constraining procedure
These constraining methods are very much useful for restraining a structure in a specific geometry model i.e. in a specific point group. I’m giving normal point groups and restrained point groups of some molecules below —
Cyclobutane (C4H8):
Normally for cyclobutane, we get D₂d point group and a puckered structure (Figure 2.7.1). But if we constrain the (C₁, C₂, C₃, C₄) dihedral angle to 180° (I restrained two opposite dihedral angle to 180°), we can get restricted cyclobutane with D₄ₕ point group (Figure 2.7.2). In restricted cyclobutane, all four atoms will be in the same plane resulting in having a horizontal plane of symmetry.
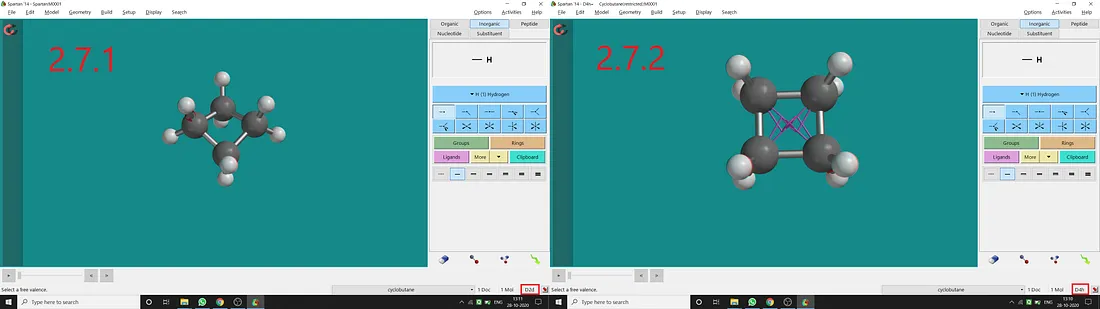
Figure 2.7: Cyclobutane normal structure and point group (2.7.1) and Cyclobutane restricted structure and point group (2.7.2)
Substituted Coronene:
If we substitute all H atoms of coronene with Methyl, we will have all Methyl substituted coronene with a C₂ point group (Figure 2.8.1). But if we restrict all the free rotations of Methyl and all the dihedral angles to have a plane of symmetry (containing all the C atoms), we will end up with a C₆ₕ point group of symmetry (Figure 2.8.2).
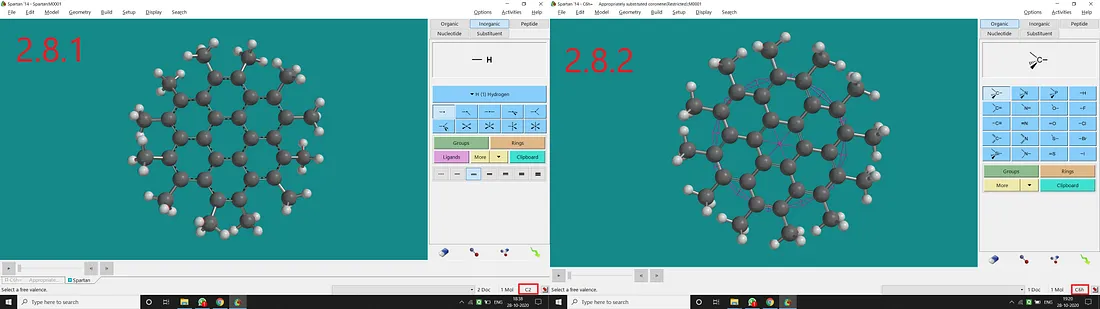
Figure 2.8: Methyl substituted coronene normal structure and point group (2.8.1) and Methyl substituted coronene restricted structure and point group (2.8.2)
Substituted Kekulene:
If we substitute all H atoms of 1, 6, 11, 16, 21 and 26 positions with the Methyl group of the Kekulene molecule, we will end up with a substituted kekulene with C₆ᵥ point group (Figure 2.9.1). Now if we restrict the dihedral angles and bond distances accordingly, we can get a restricted structure having a C₆ₕ point group of symmetry (Figure 2.9.2).
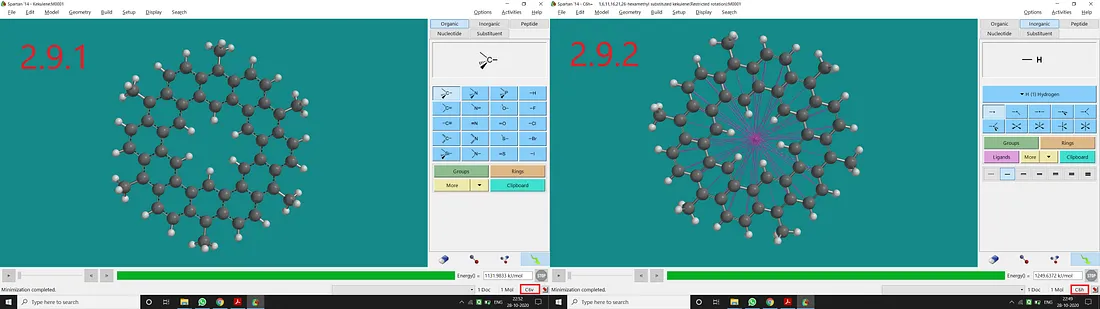
Figure 2.9: Methyl substituted kekulene normal structure and point group (2.9.1) and Methyl substituted kekulene restricted structure and point group (2.9.2)
Note:
So far what we’ve seen it’s not all. Spartan provides us with many more supported methods for helping out in the visualization of molecules in the time of reaction and computational calculations. The next and final article of this series will be on simple properties value calculation and a simple reaction kinetics study.
References:
⁕ ⁕ ⁕